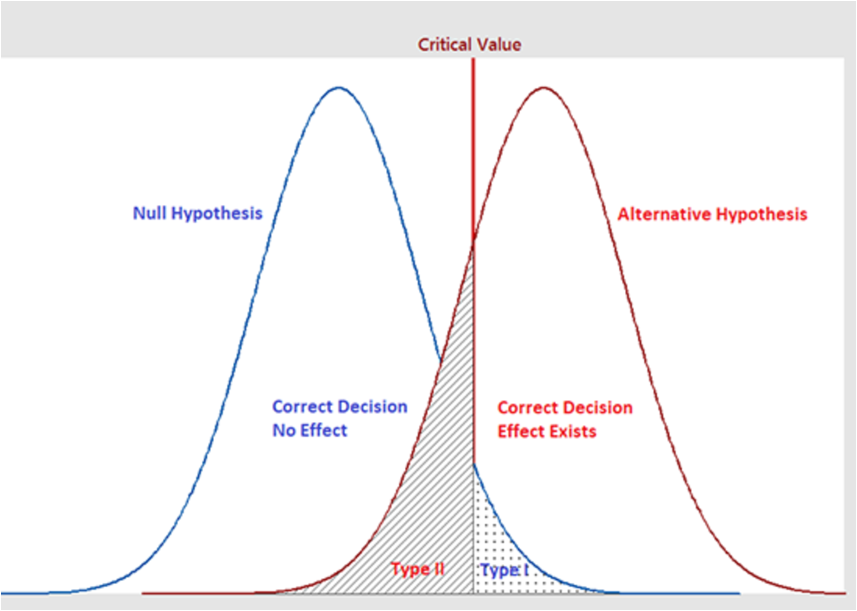
Type error
|
Test rejects Null |
Test fails to reject Null |
| Null is true |
Type 1 error- false positive |
Correct decision- no effect |
| Null is false |
Correct decision- no effect |
Type 2 error- false negative |
Example 1
Lucy can hit the target 70% of the time when she throws an axe with her right hand. She claims that the proportion,
p, of her throws that hit the target is higher than 70% when she uses her left hand.
Lucy uses the hypotheses \(H_{0}:p = 0.7\) and \(H_{1}:p > 0.7\) to test her claim. Lucy makes 100 throws and will reject the null hypothesis if the axe hits the target more than 77 times.
Let X -B(100,p) be the number of times lucy hits the target when using her left hand,
P(Type 1 error) = P(being in critical region|Ho is true)
P(Type 1 error) = \(P(X \gt 77| p = 0.7)\)
P(Type 1 error) = \(P(78\leq X \leq 100|p = 0.7)=0.04786\)
Example 2
Lucy can hit the target 70% of the time when she throws an axe with her right hand. She claims that the proportion,
p, of her throws that hit the target is higher than 70% when she uses her left hand.
Lucy uses the hypotheses \(H_{0}:p = 0.7\) and \(H_{1}:p > 0.7\) to test her claim. Lucy makes 100 throws and will reject the null hypothesis if the axe hits the target more than 77 times.
Let X -B(100,p) be the number of times lucy hits the target when using her left hand.
Given that Lucy actually hits the target 80% of the time with her left hand,
find the probability of a Type II error
P(Type II error) = P(not being in critical region|true population parameter)
P(Type II error) = \(P(X \leq 77| p = 0.8)\)
P(Type II error) = \(P(0\leq X \leq 77| p = 0.8)\)
P(Type II error) = 0.261
Example 3
In the following scenarios, decide whether a Type I error or Type II error could have occurred
(i)
A farmer is testing for a change in crop growth after trying a new fertiliser. The test concludes that there is no evidence of change at the 5% significance level.
(ii)
A dentist’s receptionist believes that the waiting times have been reduced due to a new scheduling system. They conduct a hypothesis test and will reject the null hypothesis if no more than two customers wait more than ten minutes. Exactly two customers have to wait more than ten minutes.
Example 4
The probability of getting a head when a coin is tossed is denoted by p.
This coin is tossed 12 times in order to test the hypotheses H0: p = 0.5 against H1: \(p \neq 0.5\), using
a 5% level of significance.
Given that p = 0.4
Find the probability of a type-2 error.
When p = 0.5 rejection region \(P(X\geq 10)\) or \(P(X\leq 2)\)
When p = 0.4 acceptance region \(P(3\geq X\geq 9)= 0.9137\)